La teoria delle reti idrauliche
Una
rete idraulica è un insieme di rami mutuamente collegati che
trasportano un
fluido fra uno o più punti in cui il fluido è reso disponibile (alimentazione)
ad uno o più punti in cui il fluido viene utilizzato(utenze).
Una rete
di questo tipo è una rete di adduzione , mentre in una rete di scarico
il
fluido disponibile alle utenze confluisce da queste al punto di
raccolta.
In una rete aperta il fluido circolante disponibile alle
alimentazioni
fuoriesce in corrispondenza delle utenze e lo scopo della rete è un
trasporto
di massa. In una rete chiusa al fluido è associato un trasporto
di
energia , abbinata alla massa. Pertanto il fluido ricircola fra
l’alimentazione, dove riceve l'energia termica, e le utenze , dove
questa viene
ceduta alle utenze, a parte le perdite termiche durante il percorso. La
differenza sostanziale fra circuiti aperti e chiusi è che nei secondi
l'energia
necessaria alla movimentazione del fluido è solo quella dovuta alle
perdite di
carico per attrito durante il percorso, mentre nei primi l'energia
idraulica è
anche quella necessaria al sollevamento del fluido. Nei circuiti aperti
la
movimentazione del fluido è possibile grazie ad un dislivello
favorevole o alla
presenza della pompa.
Nel caso di fluidi comprimibili come i gas, portata volumetrica e quindi massa volumica e viscosità cinematica, variano con la pressione: variazioni di pressione e perdite di carico sono mutuamente collegati. E' il caso delle reti gas in media ed alta pressione per il gas naturale.
Il calcolo delle reti idrauliche consiste nella determinazione delle portate che fluiscono nei rami delle rete, assegnate le condizioni geometriche e fluidodinamiche. Note che siano le portate ,tante quanti i rami, è possibile anche determinare le perdite di carico le pressioni e le altre grandezze fluidodinamiche. A questo scopo è opportuno introdurre una opportuna terminologia .
Il ramo. Il ramo è un tratto di tubazione (figura 1) , a diametro costante, non necessariamente rettilineo e non necessariamente formato da un singolo tratto , ma che potrebbe comprendere più tratti consecutivi. Ai fini del calcolo idraulico la schematizzazione del ramo avviene come segmento rettilineo avente un nodo iniziale ed un nodo finale. Il calcolo idraulico stabilirà , nel caso di rete magliata o ad anello il verso effettivo del flusso. In una rete, per definizione, ogni ramo è collegato ad uno o più rami.
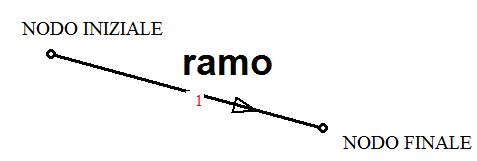
Figura 1:il ramo
Lo sviluppo geometrico di una rete. Una rete ad albero(figura 2) è rappresentata come in figura. Una rete ad albero avente una sola alimentazione è caratterizzata da un verso univoco dei rami che non può variare con il calcolo. In questa tipologia fra il numero di nodi=NN ed il numero dei rami=NR c'è la relazione=NN=NR+1. In una rete ad albero con più alimentazioni sussiste la stessa relazione ma il verso dei rami assunto inizialmente può variare.
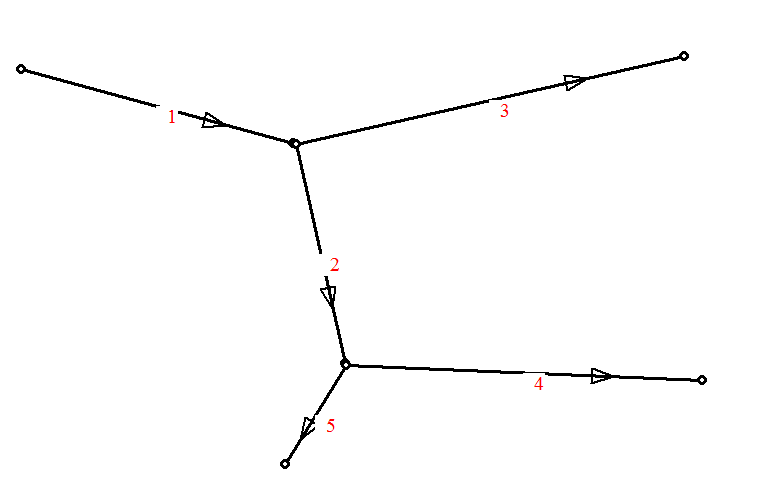
Figura 2: rete ad albero
Percorso idraulico. E' l'insieme dei rami che collegano la alimentazione alla utenza , collegati in sequenza, da un punto iniziale , l'alimentazione, al punto finale, l'utenza (figura 3).
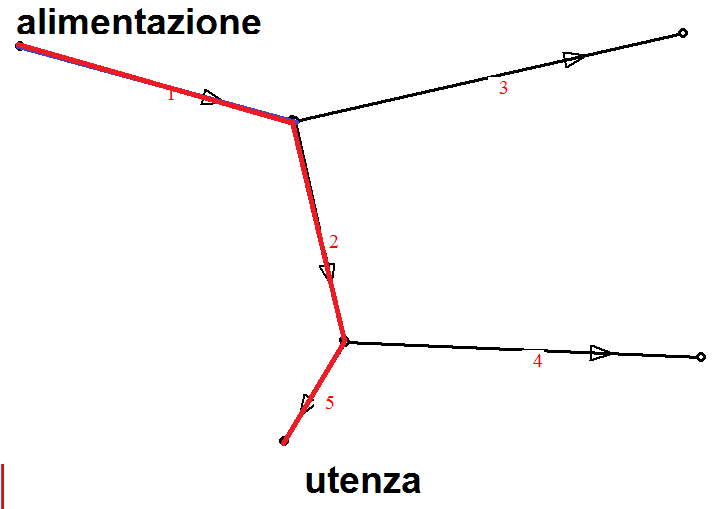
Figura 3:Percorso idraulico: nella figura i rami 1,2,5 costituiscono un percorso idraulico
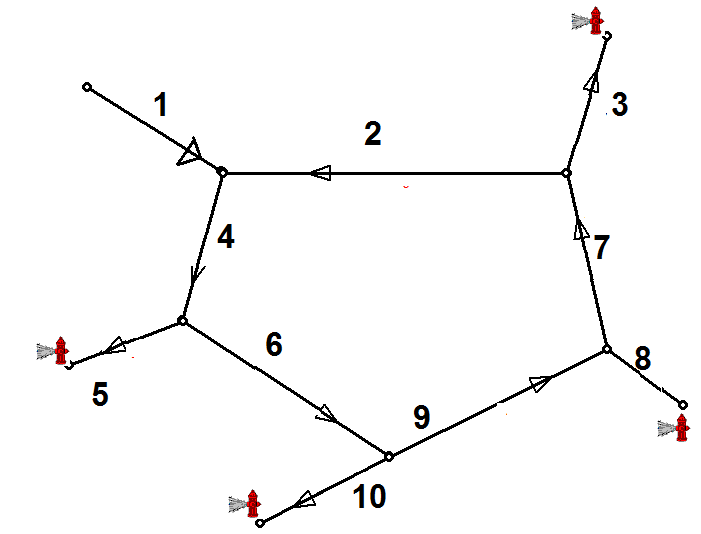
Figura
4: rete ad anello
Anello. Una rete(figura 4) in cui vi sia un sottoinsieme di rami che formano una circuitazione chiusa, ossia il ramo finale è collegato al ramo iniziale, è una rete ad anello. Non necessariamente dentro la regione spaziale nell'anello non possono essere presenti altri rami della rete. Il calcolo , nel caso di anelli singoli, suppone che vi sia un unico ramo di collegamento tra l'anello ed il resto della rete. Se gli anelli sono mutuamente collegati questi vengono denominati maglie. Le maglie mutuamente collegate fra loro costituiscono una sottorete facenti parte della rete globale(figura 5).

Figura
5:rete magliata
Ramo derivazione. La derivazione è il ramo da cui il flusso d'acqua fuoriesce.
Ramo di alimentazione. E' il ramo o i rami in cui il fluido affluisce alla rete. I rami di alimentazione e di derivazione hanno verso fissi, i primi di ingresso, i secondi di uscita, e definiti dall'utente in sede dei disegno della rete.
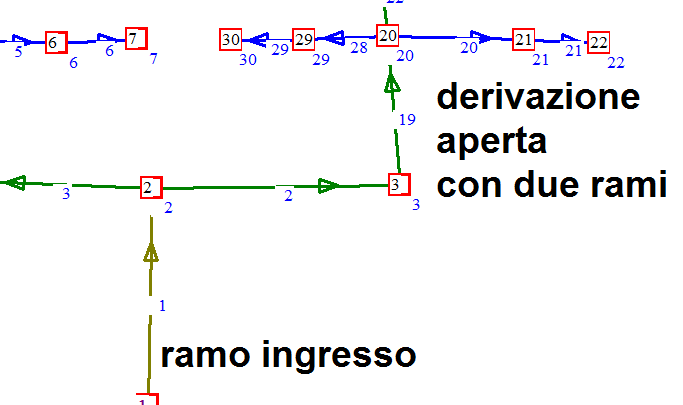
Figura
6: derivazione aperta
Le derivazioni. Le derivazioni sono costituiti(eventualmente) da più rami consecutivi verso l’uscita(figura 6) . Si suppone che il fluido, per effetto della pressione disponibile nei nodi di collegamento fra i rami, fuoriesca in corrispondenza di ciascuno nodo. Una derivazione è aperta se costituita da rami consecutivi , di cui l'ultimo non è collegato ad altri rami, a parte il precedente. Una derivazione con tre rami ha pertanto tre utenze, caratterizzate dai nodi di collegamento fra il primo ed il secondo, fra il secondo e il terzo, e dal nodo finale.
Una derivazione chiusa è formata da un insieme di rami consecutivi di cui sia il primo che l'ultimo sono collegati a punti diversi della rete. Mentre in una derivazione aperta il senso del flusso è univoco in ciascun ramo, in quella chiusa il senso non è univoco e dipende dalle condizioni idrauliche. (figura 6)
In una derivazione aperta la portata defluente dai nodi di collegamento fra i rami della derivazione è legata alla pressione disponibile al nodo secondo la relazione dell'elemento idraulico valle del nodo e generalmente. Q=k √ p. Detta Q1 la portata del ramo a monte QX la portata uscente dal nodo e Q2 quella del ramo a valle, sussiste la relazione:
Q1-QX=Q2
In una derivazione chiusa portata del ramo di monte e portata del ramo di valle possono affluire o defluire dal nodo e la relazione di cui sopra si modifica in:
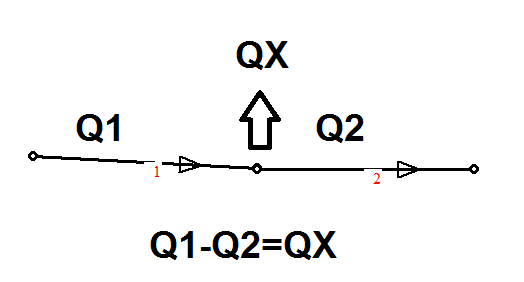
Figura 7:portate affluenti al nodo
Q1+Q2=QX dove le portate sono positive se affluenti al nodo e negative in caso opposto(figura 7).
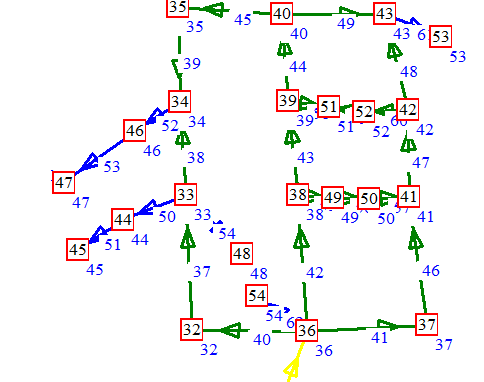
Figura
8:derivazioni aperte e chiuse
- I
rami 50,51 appartengono a una derivazione aperta
- I rami 38,49,50 ad una derivazione chiusa
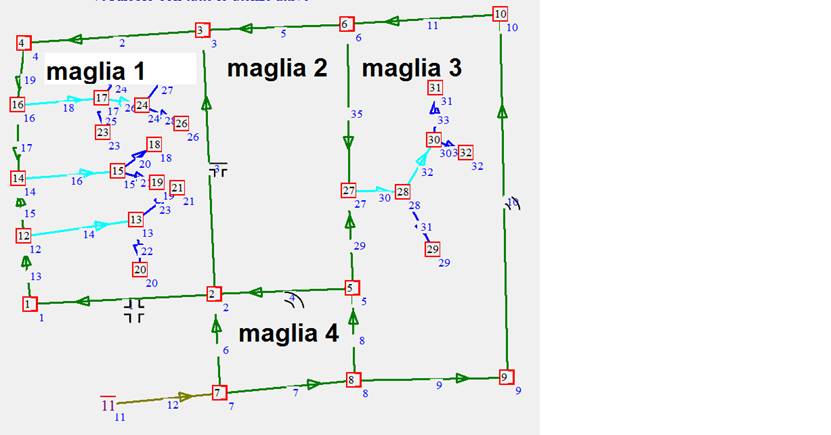
Figura
9: rami con colori diversi
La colorazione dei rami corrisponde a:
- blu:
derivazioni
- azzurro:montanti
- verde:anelli/maglie
- giallo:montanti
2
- verde
oliva: ingressi
Le
utenze possono essere localizzate nel nodo finale di un ramo di una
derivazione
aperta (esempio nodi 24,25,26) o nel nodo di collegamento dei rami
della
derivazione chiusa(nell’esempio nodi 9,10,11).Oppure nei nodi , non
appartenenti a derivazioni) della rete (nodi 70 e 69 della figura 10).
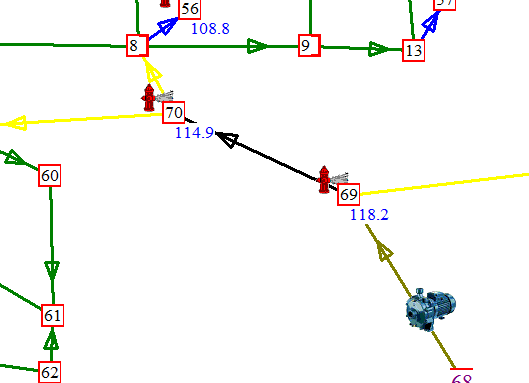
Figura
10: utenze collocate nei nodi
Utenza attiva/disattiva. Ogni utenza, individuata geometricamente nella rete, può essere ,in una scelta modalità di calcolo attiva o disattiva, se intercettata. Il calcolo della rete non comprenderà i percorsi facenti capo alle utenze non attive. In conseguenza di diverse assunzione sulle utenze attive o non attive, nelle reti che hanno sottoinsiemi ad anello o a maglie il verso dei rami si modifica in conseguenza del calcolo. Invariata è invece il verso dei rami delle reti ad albero.
La colorazione delle utenze è:
- rossa=utenza
attiva
- verde
utenza non attiva
- giallo=utenza
più sfavorita
- azzurro=utenza
meno favorita
Nella rete di figura 9 sono visibili gli elementi fondamentali di una rete aperta . Le derivazioni sono collegate a rami denominati montanti e quindi al ramo di alimentazione. Nella rete ad anello le derivazioni sono collegate a montanti di secondo livello(denominati montanti2) e quindi all'anello, oppure direttamente all'anello.
Il calcolo delle portate di una rete idraulica con il metodo di CROSS
Il
calcolo della rete consiste nel calcolo delle portate dei rami a fronte
delle
condizioni imposte. L'impostazione iniziale del calcolo assegna alle
utenze
delle portate, stabilite in base alle considerazioni impiantistiche,
che
vengono chiamate nominali. Le portate nominali delle utenze vengono
ripartite
fra i rami della rete , costituendo le portate nominali di ogni singolo
ramo,
con la scontata condizione che la portata affluente sia uguale a quella
uscente.
In alcuni tipi di calcolo questa condizione di congruenza non interviene per un diverso sviluppo del calcolo che non consiste nel determinare le portate dei rami ma i loro diametri. E' il caso delle reti gas in bassa pressione o delle rete idrosanitare o delle reti di scarico degli edifici civili.
A prescindere da questi casi particolari nel caso di calcolo delle portate è fondamentale individuare i percorsi idraulici. Nel caso di reti ad albero ogni utenza ha un singolo percorso idraulico che collega l'utenza al nodo di alimentazione. Nel caso di reti ad anello o magliate la determinazione dei percorsi idraulici diventa complessa , Partiremo da una semplice rete ad anello come in figura 11.
In questo caso il collegamento fra le utenze e l'alimentazione avviene con due differenti percorsi. Quella che può essere considerata una portata nominale consiste nell'assegnare a tutti i rami del percorso la portata nominale dell'utenza divisa per il numero dei percorsi. In conseguenza di questa operazione alcuni rami possono avere versi opposti a quelli iniziali. In ogni caso è rispettata inizialmente la congruenza delle portate confluente ai nodi. Se la rete è magliata, una volta individuati i percorsi idraulici facenti capo alle utenze, vengono determinate le portate iniziali. Il calcolo della rete consiste quindi nel calcolo di quelle che sono le portate reali a partire da quelle nominali. Le portate reali saranno quelle che rispettano le equazioni di congruenza ai nodi e le condizioni energetiche, ossia il teorema di Bernoulli applicato al percorso. In qualunque percorso idraulico l'energia idraulica iniziale, disponibile al nodo di alimentazione, sottratta delle perdite dei rami del percorso, deve essere uguale a quella del nodo caratterizzante l'utenza. In assenza di una pressione iniziale , dovuta ad esempio all'acquedotto, sarà la pompa a fornire l'energia idraulica necessaria a sopperire sia alle perdite che alla energia finale disponibile.
Il calcolo delle portate consiste nell'applicazione del metodo di Cross , opportunamente adattato, applicato al percorso idraulico e tenendo conto delle quote geometriche e piezometriche disponibili o necessarie al nodo iniziale e finale del percorso e della eventuale prevalenza della pompa inserita nel percorso. Il percorso aperto è quello che collega un ramo di ingresso ad un nodo di uscita. Nel percorso aperto intervengono le quote geometriche e piezometriche iniziali e finali. Un percorso chiuso comprende i rami dell'anello o maglia e non intervengono quote geometriche o piezometriche, essendo il nodo finale coincidente con il nodo inziale. A fronte della incertezza , in mancanza di un algoritmo relativo, per la determinazione dei percorsi aperti in una rete magliata, i percorsi chiusi di una rete magliata sono subito individuabili.
In una rete ad albero i percorsi idraulici sono tanti quante le utenze mentre in una rete magliata sono superiori.
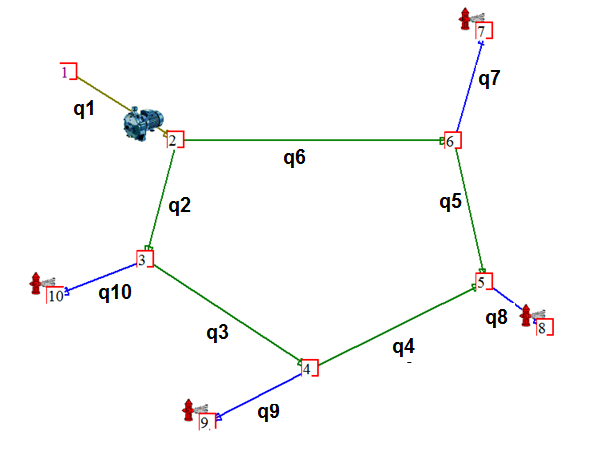
Esempio
L’esempio fa riferimento alla figura 11, al servizio di idranti che comprende un ramo di alimentazione , una pompa, e 4 idranti . La rete è ad anello con 10 rami. Nella tabella 1 sono riportate diametri e lunghezze dei rami e le quote geometriche degli idranti.
Figura 11:La rete idraulica di esempio, con la denominazione delle portate dei rispettivi rami
|
ramo |
diametro |
lunghezza |
|
|
|
|
|
mm |
m |
|
quote nodi |
|
|
1 |
68,9 |
9 |
|
nodo |
H |
|
2 |
21,7 |
7 |
|
|
m |
|
3 |
21,7 |
8 |
|
7 |
8 |
|
4 |
21,7 |
8 |
|
8 |
7 |
|
5 |
21,7 |
9 |
|
9 |
8 |
|
6 |
21,7 |
9 |
|
10 |
7 |
|
7 |
21,7 |
9 |
|
|
|
|
8 |
21,7 |
8 |
|
|
|
|
9 |
21,7 |
8 |
|
|
|
|
10 |
21,7 |
8 |
|
|
|
Tabella 1:i dati della rete
La pompa ha equazione:
H=17.630000+0.122600Q-0.010785Q2+0.000197Q3-0.000001Q4
Dove H[m H2O] Q[mc/h]
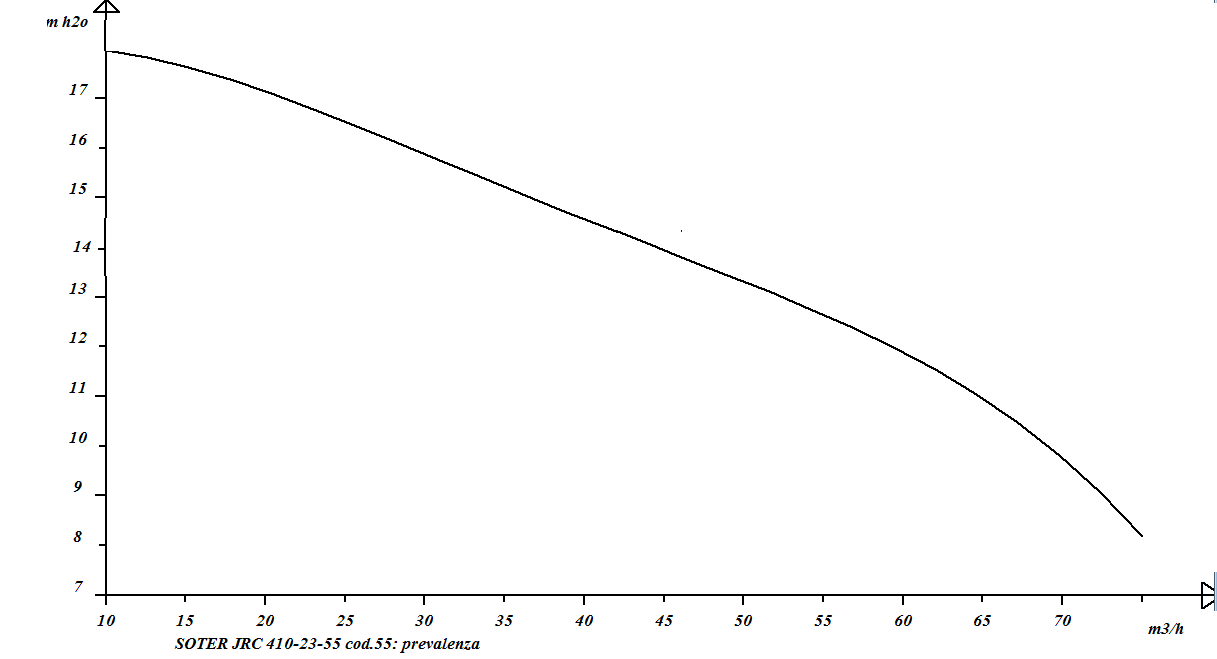
Figura 12:la curva della pompa
Nella rete , a scopo dimostrativo, vengono assunti inizialmente i versi delle portate indicati nella figura 13, anche se, secondo logica, i rami 5 e 6 dovrebbero avere verso opposto. Questo per dimostrare che il calcolo determinerà poi i versi effettivi.
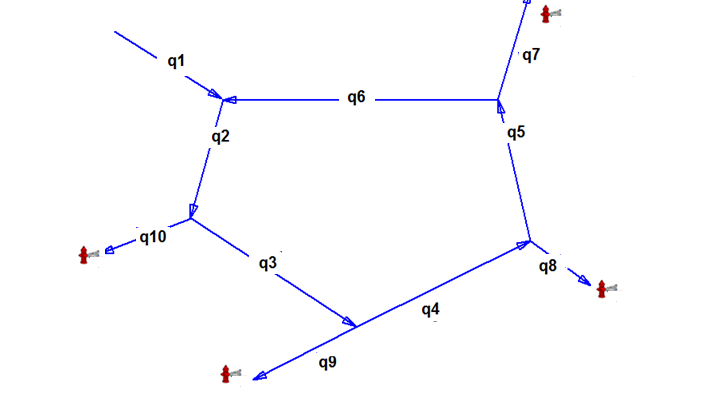
Figura
13: la
numerazione dei rami con i versi iniziali delle portate
La soluzione della rete, note che siano le caratteristiche geometriche, le quote dei nodi, la caratteristica della pompa consiste nel determinare le portate dei rami. Si introduce il concetto di percorso idraulico, l’insieme dei rami che porta dal nodo di alimentazione ai nodi terminali. Ad esempio il percorso 1 è formato dai rami 1 2,3 ,4,5, 7. Essendo la rete ad anello si individuano due percorsi per ogni terminale, il primo che percorre l’anello in un verso, il secondo in verso opposto. Il percorso 2, che porta allo stesso nodo terminale è formato invece dai rami 1,6,7.Abbiamo quindi 8 percorsi , due per ogni terminale. A questi percorsi , aperti, si aggiunge quello della maglia chiusa formata dai rami 2,3,4,5,6, per un totale di 9. Nel proseguo , ove non altrimenti specificato, le portate sono in L/m e le perdite o prevalenze in mm H2O. Per ognuno di questi percorsi va rispettato il teorema di Bernoulli che diventa ora:
· per i percorsi aperti:
[1] -Qg1-Hpompa+∑HW+Hidrante+Qg2=0
· Mentre per quello chiuso:
[2] ∑HW=0
Dove :
· Qg1 la quota geometrica del punto iniziale del percorso
· Qg2=la quota finale del percorso
· Hpompa=la prevalenza della pompa
· ∑HW= la somma delle perdite di carico dei rami che fanno parte del percorso.
|
·
Hidrante=la
caduta di pressione nell’idrante N.B
nei circuiti aperti l’energia cinetica associata alla velocità del ramo
di uscita può essere inglobata in una perdita concentrata con k=1 |
||
|
La
perdita di carico Δp
[mm H2o] nei circuiti idraulici asserviti agli impianti antincendio si
calcola con l’equazione (per acciaio): |
|
|
|
|
|
|
|
|
|
|
Δp=861529
X L x Q1,85/D4,87
la perdita degli idranti Hidrante è:
Hidrante=9810*(Q/K)2
K il coefficiente caratteristico dell’idrante(in questo caso K=80). Oltre le equazioni [1] e [2] nella rete idraulica devono essere valide le equazioni di congruenza delle portate ai nodi, ad esempio per il nodo 2 deve essere:
q1-q7+q6=0
I segni corrispondono alle assunzioni dei versi della figura 13 ( positive le portate entranti al nodo , negative quelle uscenti). Con il concetto del percorso idraulico si supera la scrittura delle equazioni di congruenza dei nodi, come si vedrà nel seguito.
Determinazione delle portate nominali
La prima fase del calcolo consiste nell’ assegnare le portate nominali delle utenze , in questo caso 120 L/m a tutti i percorsi che fanno capo alle utenze stesse. Pertanto la portata dell’utenza del nodo 7 va assegnata equamente ai percorsi 1 e 2 , e quindi ad ognuno 60 l/m. Il procedimento è il seguente.
La portata di 60 l/m viene assegnata al ramo con segno positivo se è concorde con quello del ramo iniziale 7, con segno negativo nel caso contrario. Pertanto la portata di 60 è positiva nel percorso 1 per tutti i rami . Nel percorso 2 , avendo il ramo 6 verso opposto al ramo 7, la sua portata è negativa. Automaticamente , con questa ripartizione, vengono rispettate le equazioni di congruenza ai nodi. Nella tabella 1 sono riportati i dettagli delle operazioni. La portata dei rami 5 e 6 risultano negative , ossia hanno verso opposto a quello inizialmente assunto. Pertanto l’equazione di congruenza diventa(le portate hanno segno positivo se entranti , negativo se uscenti):
nodo 2:
480(ramo 1, entrante con portata positiva)-240(ramo 2, uscente con portata positiva)-240 ( ramo 6 entrante ma con portata negativa) =0
Operando analogamente per tutti i nodi si verificherà che con questa assegnazione delle portate iniziale vengono rispettate anche le equazioni di congruenza delle portate ai nodi.
Analogamente nel nodo 6:
+240(ramo 6, uscente ma con portata negativa) -120(ramo 7 uscente con portata positiva) -120(ramo 5 entrante ma con portata negativa)=0
Tabella 2:Assegnazione delle portate nominali
|
|
rami |
|
|
|
|
|
|
|
|
|
|
percorso |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
60 |
60 |
60 |
60 |
60 |
|
60 |
|
|
|
|
2 |
60 |
|
|
|
|
-60 |
60 |
|
|
|
|
3 |
60 |
60 |
60 |
60 |
|
|
|
60 |
|
|
|
4 |
60 |
|
|
|
-60 |
-60 |
|
60 |
|
|
|
5 |
60 |
60 |
60 |
|
|
|
|
|
60 |
|
|
6 |
60 |
|
|
-60 |
-60 |
-60 |
|
|
60 |
|
|
7 |
60 |
60 |
|
|
|
|
|
|
|
60 |
|
8 |
60 |
|
-60 |
-60 |
-60 |
-60 |
|
|
|
60 |
|
|
480 |
240 |
120 |
0 |
-120 |
-240 |
120 |
120 |
120 |
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Figura
14: le portate nominali con i versi effettivi
Si sottolinea che il concetto di percorso idraulico si presta bene a considerare il caso che alcun idranti siano considerati inattivi o meglio vengano presi in considerazione solo gli idranti più sfavoriti o meno favoriti. Nel caso considerato, il calcolo determina, con tutti gli idranti attivi, quelli facenti capo ai nodi 8 e 9 quelli più sfavoriti. Pertanto basta considerare , nella tabella 2, nullo il loro contributo di portata. Successivamente vengono esclusi dal calcolo i percorsi facenti capo a questi idranti.
Calcolo iterativo con l’equazione [1] Per procedere alla prima iterazione per il percorso 1 si compila la tabella 2.Il ramo 6 ha una portata iniziale negativa e quindi sarà negativa la sua perdita. La formulazione originaria del metodo di CROSS è fatta per le maglie chiuse, per cui deve valere l’equazione [2]. Il metodo suppone che la perdita di carico sia esprimibile con l’equazione Δp= K Q2 per cui l’equazione [2] diventa: ∑ Ki Qi2 =0. Se le portate non soddisfano questa uguaglianza si aggiunge un incremento di portata Δ tale che : ∑ (Ki Qi+ Δ) 2 =0 Sviluppando e trascurando il termine Δ2 si ottiene: ∑ Ki Qi2+ 2Ki Δ=0 per cui il termine correttivo Δ vale:
[3] Δ =-0,5 ∑ Ki Qi2/|∑ (Ki Qi|
Si modifica il metodo di Cross originario. Al numeratore si aggiungono le perdite di carico , le quote geometriche(con segno positivo la quota geometrica finale e negativa quella iniziale) e la prevalenza della pompa ,con segno negativo . I valori dei termini Ki Qi relativi ai rami vengono determinati in base alla uguaglianza: Ki Qi Qi= HW per cui : Ki Qi=HW/ Qi , che vengono rinominati come HQi . Il termine 0,5 viene modificato con 0,15. Pertanto il numeratore NUM diventa:
NUM =[ ∑ HWi-QG1+QG2+Hidrante-Hpompa]
Mentre il denominatore diventa:
DEN= ∑ |HQi |+|Hidrante/Qidr|+|Hpompa/Qpompa|
il valore di Δ dell’equazione [3] diventa in questo caso:
[4] Δ =-0,15 NUM/DEN
Tabella 3:calcolo del percorso 1 prima iterazione
Il segno
della prima colonna indica la concordanza dei versi dei rami rispetto a
quello iniziale. Pertanto se il verso è positivo la perdita relativa
sarà positiva e viceversa. In questo caso risulta negativa la perdita
del ramo 5. Per il percorso 1, prima iterazione risulta: · Qg1=0 · Hpompa=-16030 · ∑HW=+63133 · Hidrante =+22173 · QG2=+8000 Pertanto risulta : NUM=0+63133+22173-16030+8000=77176 DEN=822,65 Δ =-0,15 x NUM/DEN=-14,07 L/m
Il coefficiente 0,15 differisce da quello originario del metodo per tener conto dei termini non lineari quali la quota geometrica e la prevalenza della pompa , ed è quello che assicura una buona convergenza del metodo. Valori di questa costante eccessivi potrebbero determinare una instabilità del calcolo. Pertanto è preferibile aumentare il numero di iterazioni piuttosto che rischiare , in base ai dai assunti, che il procedimento non converga. Ad esempio, nel caso specifico, è evidente che il termine correttivo non può superare, con segno negativo, la portata nominale dell’idrante , facendo risultare la portata stessa dell’idrante negativa. Inoltre , in funzione della caratteristica della pompa, la portata della pompa deve rimanere nel range per cui viene definita la sua curva caratteristica. Inoltre deve essere verificato che: Hmax pompa+QG1-QG2>0 Se
questa condizione non è verificata non vi è incontro fra la curva H-Q
del circuito idraulico e quella della pompa e quindi non c’è soluzione. |
|
q |
D |
L |
|
HW |
HW |
HQ |
Qnuova |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Per
il percorso 9, maglia chiusa risulta:
Tabella 4:percorso 9(maglia chiusa) prima iterazione
|
|
ramo |
q |
D |
L |
|
|
HW |
HQ |
Qn |
|
- |
6 |
240 |
21,7 |
9 |
|
|
-60862 |
254 |
225,9 |
|
- |
5 |
120 |
21,7 |
9 |
|
|
-16883 |
141 |
105,9 |
|
+ |
4 |
0 |
21,7 |
8 |
|
|
0 |
0 |
-14,1 |
|
+ |
3 |
120 |
21,7 |
8 |
|
|
15007 |
125 |
105,9 |
|
+ |
2 |
240 |
21,7 |
7 |
|
|
47337 |
197 |
225,9 |
|
|
|
|
|
|
|
|
-15401 |
717 |
|
∑HW=-15401
Pertanto risulta NUM=-15401
DEN=717
Δ =-0,15 x NUM/DEN=-3,22 l/m
Il calcolo iterativo si sviluppa per ognuno dei 9 percorsi , nell’esempio per 9 iterazioni, in cui il Δ medio(media dei Δ relativi a ciascun percorso) è:
iterazione
1 Δ = 0.032
2 Δ = 0.051
3 Δ = 0.180
4 Δ = 0.162
5 Δ =-0.183
6 Δ =-0.136
7 Δ =-0.180
8 Δ =-0.092
9 Δ =-0.011
Tabella 5:portate dei rami ad ogni iterazione
Iterazioni del calcolo
Ra iterazioni
Mo 1 2 3 4 5 6 7 8 9
1 480.000 334.681 245.793 194.746 167.779 154.696 148.731 146.154 145.087
2 240.000 170.917 127.872 102.791 89.346 82.689 79.551 78.115 77.452
3 120.000 82.261 58.587 44.974 38.042 35.024 33.933 33.673 33.708
4 0.000 -1.305 -2.391 -2.624 -2.025 -0.941 0.211 1.220 2.008
5 -120.000 -81.456 -58.529 -45.425 -38.330 -34.668 -32.843 -31.956 -31.539
6 -240.000 -163.763 -117.921 -91.955 -78.433 -72.007 -69.179 -68.039 -67.635
7 120.000 82.308 59.392 46.530 40.104 37.340 36.336 36.082 36.097
8 120.000 80.151 56.138 42.801 36.305 33.726 33.054 33.176 33.547
9 120.000 83.566 60.978 47.598 40.067 35.965 33.722 32.453 31.700
10 120.000 88.657 69.285 57.817 51.304 47.665 45.618 44.442 43.744
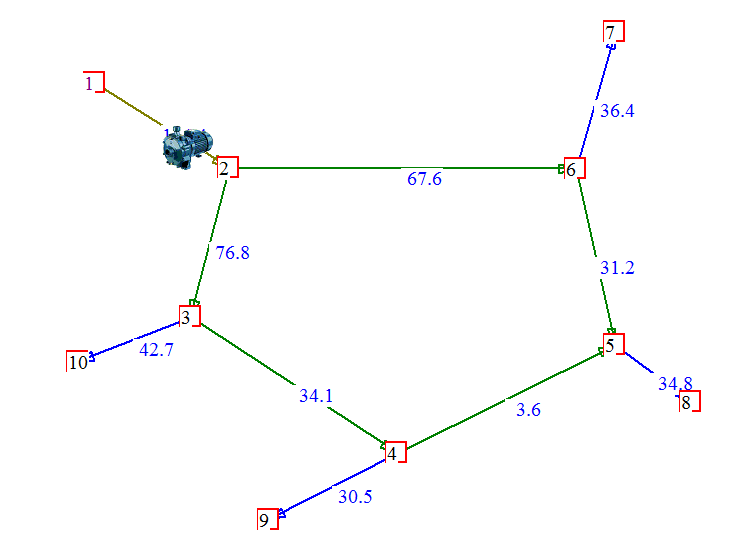
Figura 15 :le portate finali
|
|
LE
VERIFICHE Relativamente
ai percorsi 1 e 9 si verificano con gli stessi metodi delle
tabelle 3 e 4 con i risultati finale delle portate. Pertanto la tabella
3 diventa la tabella 6 e la tabella 4 la tabella 7 |
|
|
|
|
ramo |
q |
D |
HW |
HW |
HQ |
Qnuova |
|
+ |
1 |
144,41 |
68,9 |
86 |
86 |
0,59 |
130,34 |
|
+ |
2 |
76,8 |
21,7 |
5751 |
5751 |
74,88 |
62,728 |
|
+ |
3 |
34,1 |
21,7 |
1464 |
1464 |
42,92 |
20,028 |
|
+ |
4 |
3,6 |
21,7 |
23 |
23 |
|
-10,47 |
|
- |
5 |
31,2 |
21,7 |
1397 |
-1397 |
44,77 |
17,128 |
|
+ |
7 |
36,4 |
21,7 |
1858 |
1858 |
51,04 |
22,328 |
|
|
pompa |
144,4 |
|
-17962 |
-17962 |
37,42 |
|
|
|
utenza |
36,4 |
|
2030,9153 |
2031 |
55,79 |
|
Tabella 6:il prospetto del percorso 1 relativo all’ultima iterazione
Pertanto :
· ∑HW =7784
· QG2= 8000
· Perdita idrante=2030
· H pompa= 17962
NUM= 7784+8000+2030-17962=-147
DEN=∑HQ=307,41
Δ =-0,071
Per il percorso 9:
|
|
ramo |
Q |
D |
L |
|
|
HW |
HQ |
Qn |
|
- |
6 |
67,6 |
21,7 |
9 |
|
|
-5839 |
86,3 |
53,5 |
|
- |
5 |
31,2 |
21,7 |
9 |
|
|
-1396 |
44,7 |
17,1 |
|
+ |
4 |
3,6 |
21,7 |
8 |
|
|
22 |
0,000 |
-10,5 |
|
+ |
3 |
34,1 |
21,7 |
8 |
|
|
1464 |
42,9 |
20,0 |
|
+ |
2 |
76,8 |
21,7 |
7 |
|
|
5750 |
74,8 |
62,7 |
Tabella 7:verifica percorso 9
Per cui ∑HW =1,1163 DEN=248,947 Δ =0,0007
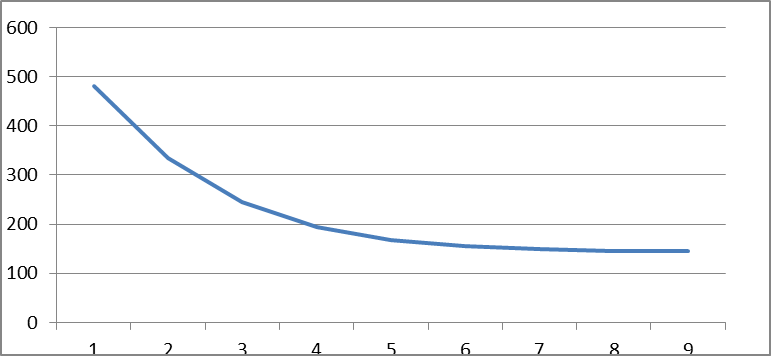
Figura 16 La portata del ramo 1 nelle successive iterazioni
Approfondimento sulla ricerca dei percorsi idraulici
Un
percorso idraulico
collega una utenza alla alimentazione ed è l’insieme dei rami che
partono dalla
alimentazione ed arrivano alla utenza. Con riferimento alla figura 1 le
utenze
sono localizzate nei nodi 7,11,12,,9,4,5. I rami interessati
6,10,11,8,,3,4
sono pertanto definiti come derivazioni
aperte .Il percorso che fa capo all’utenza del nodo 11
ha come primo ramo la derivazione ,ramo 11.Il
percorso prosegue dal nodo 10 nel quale convergono tre rami: 10,11,9.
Per la
ricerca del ramo successivo collegato al nodo si esclude
il ramo di partenza e tutte le derivazioni.
Il ramo successivo è quindi il ramo 9
che viene definito come montante. Al
ramo 9 è collegato, escludendo la derivazione del ramo 8, il ramo 7 e
così via
fino al nodo2, che fa capo al ramo di alimentazione che è il ramo 1.
L’insieme
dei rami 9+7+5 fa parte del montante 1.
Il percorso della utenza che fa capo alla derivazione 1 è composta dai
rami:
11+9+7+5+1
La
derivazione del ramo 8
si collega al montante 1 a partire dal nodo 8 .Il relativo percorso è
composto
dai rami:8+7+5+1. La derivazione del ramo 3 si collega al ramo 2 che è
un montante
che diventa montante 2.Il percorso
relativo è formato dai rami:8+2+1. Analogamente per le derivazioni 6 e
4.
Abbiamo
quindi 6 rami
classificati come derivazioni (in blù), 4
rami
classificati come montanti raggruppati come montante 1 e montante2 ed
un ramo
di alimentazione (ramo 1).
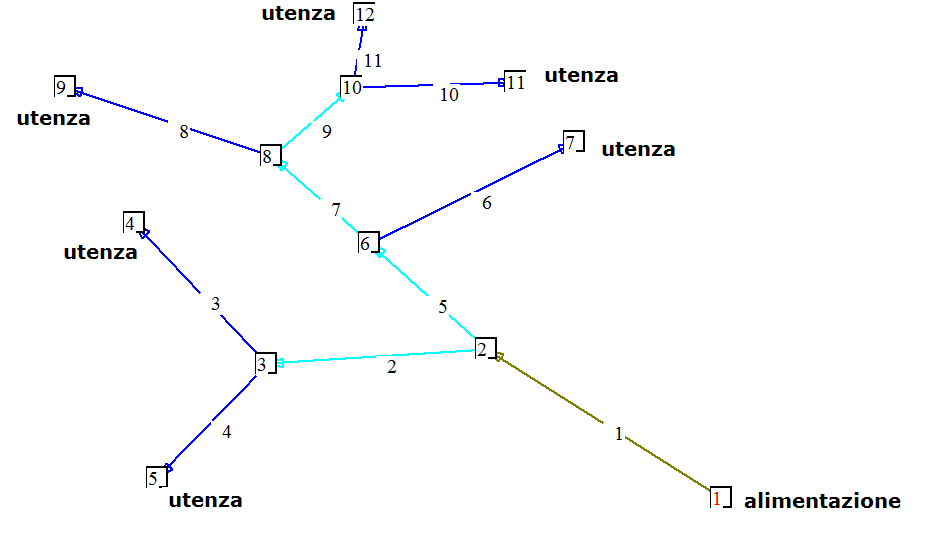
Figura
17:la rete
Figura
18:alimentazione,utenze
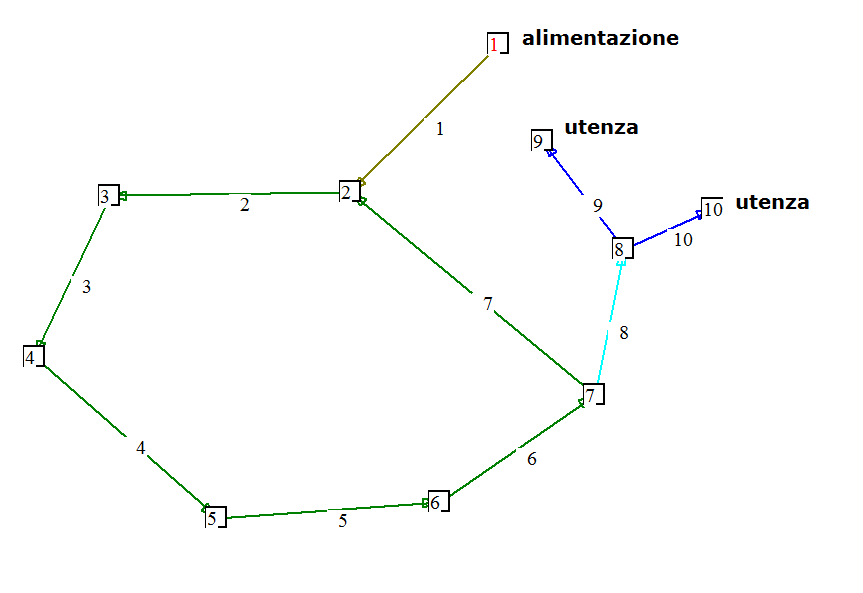
Nel caso di geometrie ad anello,figura 18 il ragionamento relativo all’utenza del ramo 9 è analogo al precedente per i rami 9+8.
Nel nodo 7 i percorsi possibili per arrivare alla alimentazione sono 2: i rami 7+1 e 6+5+4+3+2+1.
Complessivamente
all’utenza del nodo 9 competono 2 percorsi:
9+8+7+1
9+8+6+5+4+3+2+1
Figura
19:la rete con le definizioni
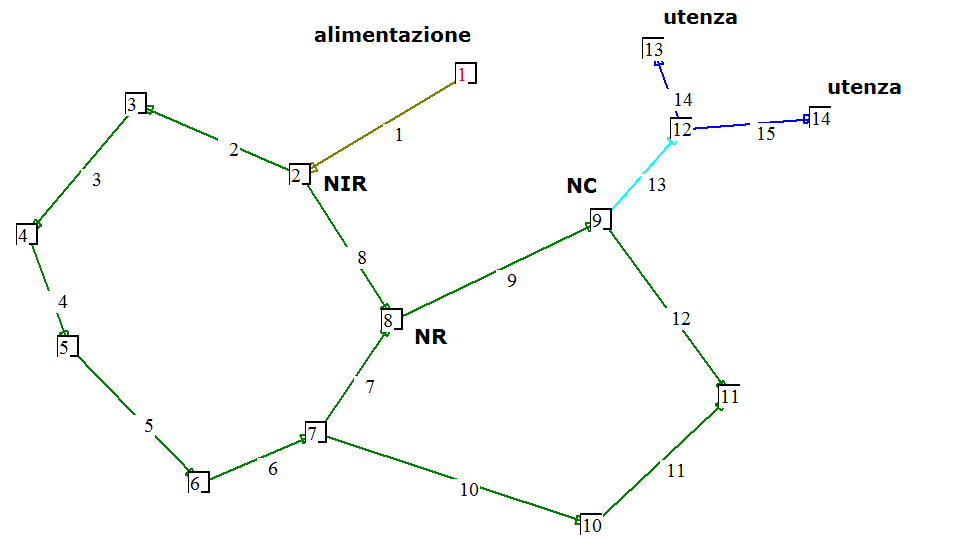
Nel
caso di più anelli fra
loro collegati o maglie bisogna
definire(figura 19) :
·
NC=
il nodo di collegamento della utenza
alla maglia 1
·
NIR=
nodo di alimentazione della rete
·
NR=
il nodo della maglia più vicino al nodo
NIR, determinato fra quelli che collegano le 2 maglie, in questo caso i
nodi 7
ed 8.
Il
percorso relativo alla utenza
è formato (fino al nodo NR) da:
14+13+9
14+13+12+11+10+7
Ed
infine il percorso più
breve fra il nodo NR e NIR in questo caso il ramo 8 ed ,ultimo, il ramo
1.Complessivamente:
14+13+9+8+1
14+13+12+11+10+7+8+1
Figura
20:le sottoreti
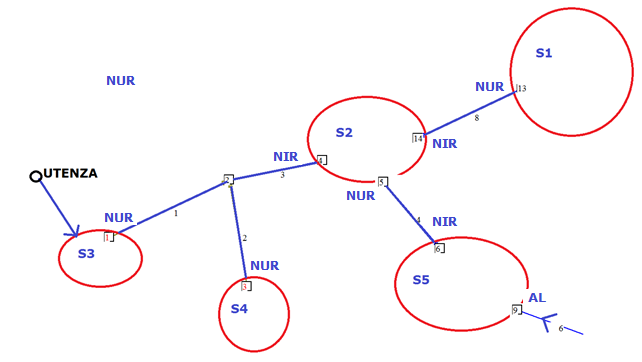
Consideriamo
il caso più
complesso di più maglie fra loro collegate e denominate sottoreti come
quelle schematizzate come circoli S1..S5(figura 20). Per la
unica utenza collegata alla sottorete S3 valgono tutte le
considerazioni fatte
precedentemente fino al nodo 1 o NUR ,nodo uscita sottorete. Il ramo 1
è quindi
un ramo di uscita. Analogo discorso per la sottorete S4 con il ramo di
uscita 2
e S1 con il ramo di uscita 8. Questi rami sono classificati come montanti2.Ogni sottorete può avere più
rami di ingresso ma un solo ramo di uscita o , in alternativa, essere
collegata
all’alimentazione. Pertanto per la sottorete S2 il ramo 8,proveniente
dalla
sottorete S1 è un ramo di ingresso e di ingresso il nodo NIR relativo.
La
sottorete S2 ha 2 ingressi ed una uscita. Il collegamento fra S3 ed S2
avviene
con i rami montante2 1+3 .Analogamente fra S4 e S2 con i rami 2+3.Il
percorso
che porta dall’unica utenza definita nello schema si compone delle
seguente
fasi successive:
·
i
rami dalla derivazione fino al nodo 2 .
·
I
rami di collegamento alla sottorete S2
=1+3
·
I
rami dal nodo di ingresso della sottorete
S2 al nodo di uscita della stessa sottorete.
·
I
rami che collegano S2 e S5.
·
I
rami del percorso più breve fra il nodo
NIR della sottorete al nodo di alimentazione
Figura
21:rete con derivazioni
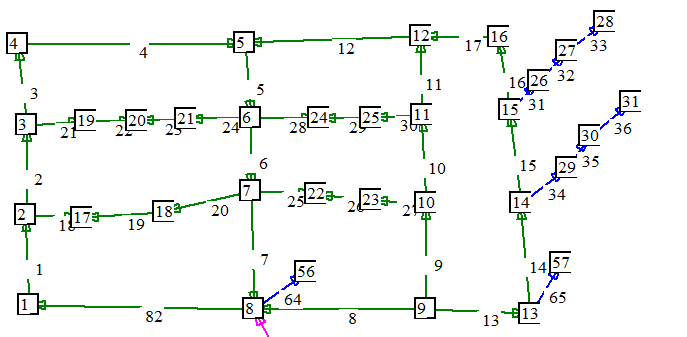
La
rete di figura 21
rappresenta una configurazione parzialmente a griglia, tipica degli sprinklers, in cui le utenze sono collocate nei
nodi
17,18 19,20,21
24,25 e 22,23, oltrechè
nelle derivazioni ad albero.
L’insieme
di rami 18+19+20
e simili rappresentano una derivazione
chiusa. I rami della derivazione chiusa sono nello stesso tempo
facenti
parte di maglie chiuse. Consideriamo l’utenza relativa al nodo 19.
L’utenza fa
parte di una maglia chiusa formata dai rami 21+22+23+24+6+20+19+18+2.
Il nodo
di riferimento della maglia è il nodo 7, quello più vicino alla
alimentazione
nodo 8. L’utenza viene quindi sdoppiata:
la
prima utenza fittizia ,
fino al nodo 7,è composta dai rami:21+2+18+19+20. La seconda dai
rami:22+23+24+6.
Ad
entrambe i percorsi si
aggiunge il ramo7 e successivi fino all’alimentazione.
Riassumendo
i percorsi
idraulici delle reti sono costituite dai percorsi
aperti che vanno dalle utenze all’alimentazione . Se una utenza non
è
definita il relativo percorso non viene considerato. Ad esempio se nel
nodo 57
non viene definita una utenza il percorso che fa capo al ramo 65 non
esiste ed
il relativo ramo è in pratica un ramo “morto”.
A
questi percorsi aperti
si aggiungono tutti i percorsi chiusi formati dalle maglie chiuse,
sette nel
caso della figura 21.
Figura
22:le maglie
La
ricerca delle maglie.
Per maglie si intende l’insieme dei rami ,
escluse le derivazioni, i montanti, i montanti2 che formano una
circuitazione
chiusa che non contiene altri rami al suo interno. La ricerca delle
maglie è
indipendente dai versi assunti dei rami.La
ricerca
delle maglie parte dai punti TRIPLI, nodi in cui convergono 3 o più
rami(figura
22).
Il
nodo 2 è un punto
triplo, il nodo 8 non lo è. Partendo dal nodo 2 si considera come
appartenente
alla maglia da individuare uno qualsiasi dei rami uscenti, ad esempio
il ramo
2. Il ramo successivo potrebbe essere 3 oppure 11 oppure 8. Si assume
quello
formante un angolo minore con il ramo di
partenza , in questo caso 8. I rami 2+8 hanno ora un verso antiorario,
che
prescinde dalla orientazione dei singoli rami. Il ramo successivo sarà
quello
che conserva la stessa orientazione e cioè il ramo 7. I rami 12 e 13
vanno
infatti in verso orario. Ovviamente il ramo che chiude la maglia è il
ramo 6.Ripartendo
dal nodo 2 si considera ora il ramo 6. Con ragionamento analogo si
costruisce
una maglia 6,7,8,2 che è uguale a quella precedente e quindi viene
esclusa.
Ripetendo per ogni nodo triplo si individuano le 5 maglie.
La
rete distingue i rami
che fanno parte delle maglie e i rami esterni, in questo caso il ramo
17.
Infatti
per ogni punto
triplo vale la relazione per i nodi esterni( 2 e 4 in questo caso)
NR=NM+1
Dove
NR è il numero di
rami confluenti al nodo e NM il numero di maglie collegate al nodo.
Per
i nodi interni (3 in
questo caso):
NR=NM
Al
nodo 7, esterno ,
invece:
NR=NM+2
Quindi
al nodo 7 uno dei 5
rami è un ramo esterno, di ingresso o di uscita dalla rete. Per
individuare il
ramo esterno si osserva che:
al
nodo 7 convergono le
maglie 2,4,5. I rami 7,8,12,13 appartengono tutti alle maglie indicate.
Il ramo
17 non appartiene
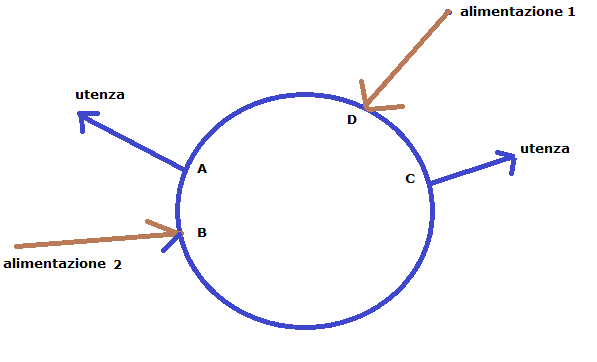
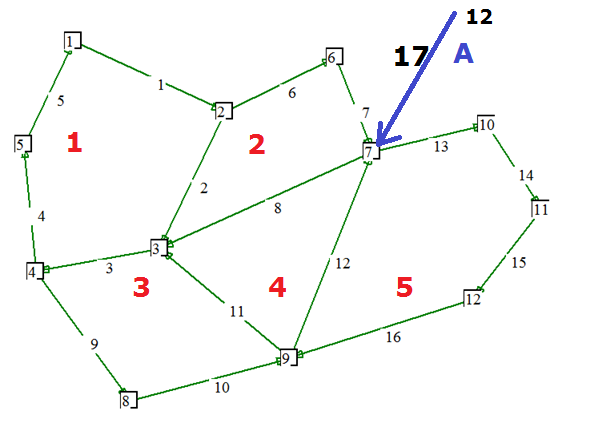
Più alimentazioni
Nel
caso di più
alimentazioni(figura 23) i percorsi
vengono costruite una alimentazione per volta. Pertanto prima si
costruisce i
percorsi che vanno dalle utenze al nodo D, prima alimentazione,
successivamente
i percorsi che vanno dalle stesse utenze al nodo B, seconda
alimentazione.
I percorsi effettivi
Figura
24: Rete
ad anello con 3 alimentazioni
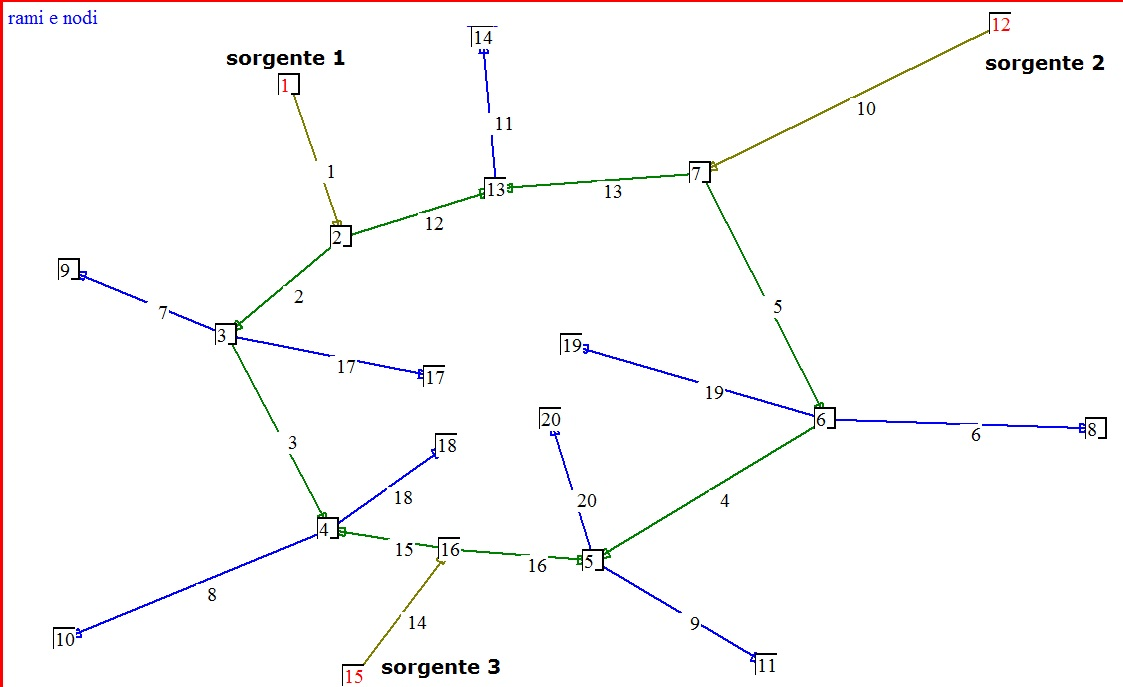
Abbiamo
detto che i percorsi
idraulici collegano le utenze alla o alle alimentazioni. A seconda che
la rete
sia ad albero , ad anello, o magliata il
software
costruisce i percorsi idraulici secondo una propria metodologia,
ricavando poi
le portate della rete reali e quindi determinando i versi effettivi
delle
portate dei rami. Può risultare , ed è facile che sia così, che i
percorsi
idraulici assunti non siano più costituiti da rami in cui il verso
delle
portate abbia sempre lo stesso verso . Con riferimento alla figura
24,il
percorso idraulico iniziale che collegava la sorgente 3 con l’utenza
del nodo 8
era costituito dai rami 14+16+4+6. I rami 14 e 16 sono collegati
idraulicamente
in modo consecutivo, ossia parte della portata del ramo 14 affluisce al
ramo
16, ossia il nodo finale effettivo del ramo 14 coincide con il nodo
iniziale
effettivo del ramo 16. Parliamo di nodo iniziale effettivo e nodo
finale
effettivo, quelli cioè risultanti dalle portate effettive. Il ramo 16 e
il ramo
4 sono collegati diversamente: il nodo finale del ramo 16 è il nodo
finale del
ramo 4. In sostanza l’insieme iniziale dei rami 14+16+5+6 non è un
percorso
effettivo. Lo è invece l’insieme dei rami
10+5+6 .
Pertanto
il numero di
percorsi assunti differisce da quelli effettivi ,ed è generalmente
minore , e
possono essere costituiti anche in modo difforme da quelli iniziali.
Nel caso
di figura i percorsi iniziali sono 55 mentre quelli effettivi 14.Nel
caso di
più alimentazioni ogni utenza può essere
alimentata da una o più alimentazioni con un contributo diverso.
Per
determinare la ripartizione delle portate delle sorgenti alla singola
alimentazione occorre stabilire quali sono i percorsi effettivi. La
portata
della sorgente che arriva alla singola utenza va determinata in base
alle
derivazioni , che sottraggono portata.
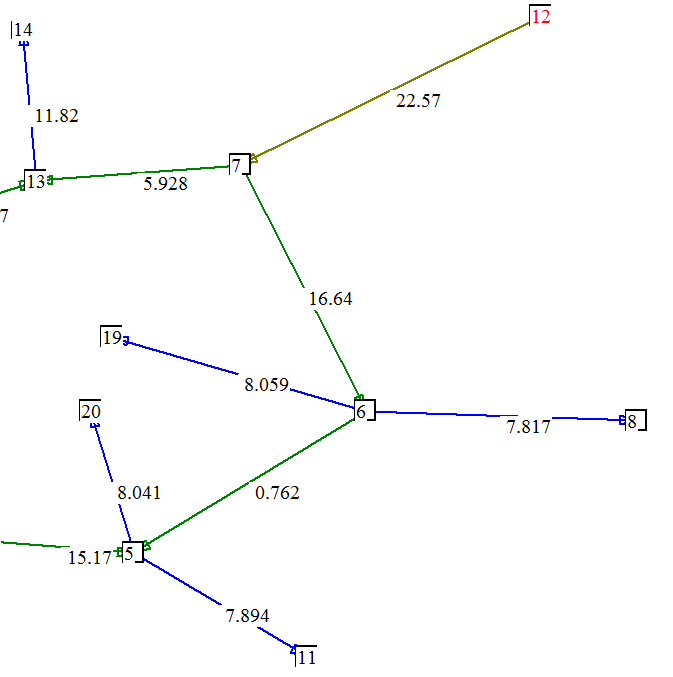
Figura
25: le portate
delle utenze
Consideriamo
il percorso
relativo ai rami 10+5+6(figura 25) .La sorgente 2 produce una portata
di 22.57
ma nel nodo=7 si separa la portata=5.928 , per cui al ramo 5 arriva
solo la portata
=22.57-5.928=16.64 . Nel nodo 6 una parte della portata va all’utenza
del
nodo=19 , una parte prosegue sul ramo 4 e solo la
differenza=16.64-8.059-0.762=7.817 va all’utenza del nodo 8.Questa
utenza
riceve il 100% della sua portata dalla sorgente 2.Diversa è la
situazione
dell’utenza del nodo=14 in cui la portata affluisce sia dalla sorgente
1 che 28(figura
26) .Il riassunto della ripartizione è riportato nel prospetto 9.
Tabella
9:Riassunto prospettico delle portate delle utenze
suddivise
per
sorgente di alimentazione
Sorg=1
Sorg=2
Sorg=3
nodo 1
12
15
ramo 1
10
14
Ute..Ramo..Sorg=1
Sorg=2
Sorg=3
Q[mc/h] %
Q[mc/h]
% Q[mc/h]
%
1 6
0.000 0
7.817
100 0.000
0
2 9
0.000
0 0.377
5
7.516 95
3 8
0.555
7 0.000
0
7.237 93
4 7
7.835
100 0.000
0
0.000 0
5 19
0.000
0 8.059
100
0.000 0
6 20
0.000
0 0.385
5
7.657 95
7 18
0.623
7 0.000
0
8.119 93
8 17
7.740
100 0.000
0
0.000 0
9 11
5.887
50 5.928
50
0.000 0
TOTALE 22.640
22.567 30.530