LE VALVOLE DI REGOLAZIONE
Nelle valvole di regolazione si definisce la grandezza
KV come:
[1] Q=KV rad( DP)
dove :
rad=radice quadrata
DP e’ espresso in bar e la portata Q in mc/h
KV quindi è la portata che passa nella valvola con una
caduta di pressione di 1 bar.La valvola ha capacita’
di regolazione della portata variando la strozzatura
nella stessa attraverso il movimento lineare di un
otturatore che percorre uno spazio chiamato corsa.In
condizioni di completa apertura si ha una corsa del
100%.La relazione fra il valore di KV e la corsa puo’
essere di vario tipo, ad esempio lineare:
KV= corsa KVMAX
In una valvola a tre vie lo stesso stelo ha due
otturatori e mentre su una via vi e’ una certa corsa
sull’altra si ha una corsa complementare.
Si fa
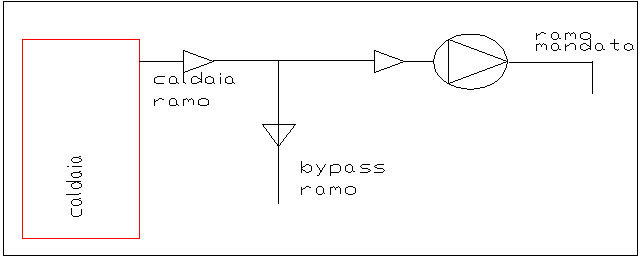
riferimento alla figura 1 dove con il pedice 1 si
intende il ramo caldaia,con il pedice 2 quello di
bypass,3 il ramo di mandata.
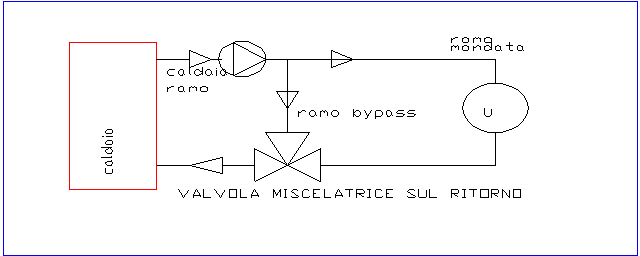
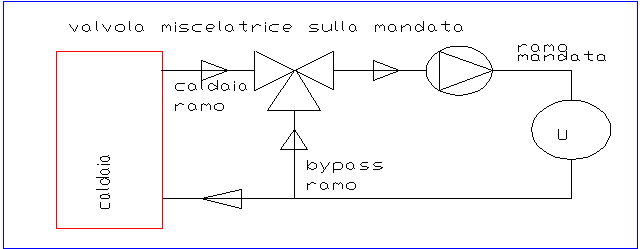
figura 1 : il circuito con valvola miscelatrice
Sul ramo caldaia si ha :
KV1=corsa KVMAX
Sul ramo di bypass :
KV2=(1-corsa) KVMAX
Poiche’ la caduta di pressione sui ramo 1 e sul ramo 2
è uguale ,essi fanno capo agli stessi nodi,fra le
portate Q1 e Q2,trascurando le perdite di carico dei
rami,si ha la relazione:
[2] Q1/Q2=corsa/(1-corsa)
Inoltre,poiche’:
Q3=Q1+Q2
le portate Q1,Q2 sono legate a Q3:
Q1=corsa x Q3
Q2=(1-corsa)x Q3
Si puo’ dimostrare che nel circuito di figura 1 , a
miscelazione ,la portata Q3 e’ costante,nell’ipotesi
di perdite di carico trascurabili nei rami caldaia e
bypass.Per l’equilibrio idraulico dei rami bypass e
mandata e’ infatti:
Q2^2
HP(Q3)+h3(Q3)- --------------
( 1-corsa)KVmax
dove:
HP(Q3)=prevalenza della pompa ,funzione della sua
portata Q3
h3(Q3)=perdite di carico del ramo mandata
Q2^2/(1-CORSA) KV =perdita di carico del ramo di
bypass,secondo la [1]
ma poiche’ :
Q2=(1-corsa) Q3
sostituendo si ha:
HP(Q3)+h3-Q3^2/KVmax=0
Quindi l’equilibrio idraulico non e’ influenzata dalla
corsa e la portata Q3 rimane quindi costante al
variare della corsa.L’equilibrio e’ comunque
influenzato dal valore di KVmax.
LA REGOLAZIONE CON VALVOLA MISCELATRICE.
Facciamo sempre con riferimento alla
schema di figura 1 con l’intenzione di studiare un
circuito idraulico reale ,sia con radiatori che con
ventilconvettori ,con valvola miscelatrice.La portata
Q1 a temperatura di mandata della caldaia TC ,
supposta costante, viene miscelata con la portata Q2 a
temperatura TR ,di ritorno dall’utenza.La portata Q3
somma di Q1 e di Q2 avra’ una temperatura risultante
TM,temperatura di mandata, data dalla seguente
eguaglianza:
Q1 TC +Q2 TR =Q3 TM
D’altro canto l’emissione termica complessiva dei
radiatori rappresentanti l’utenza è:
EMISS(TM,TR)=1,163 Q3 (TM-TR)
Dove l’espressione EMISS(TM,TR) indica che l’emissione
del corpo termico e’ funzione della temperatura di
mandata TM e di quella di ritorno TR.Queste due
equazioni non possono essere risolte direttamente
:assunto un valore iniziale di TM si ricava TR
corrispondente sostituendo entrambi i valori nella
seconda si ricava un successivo successivo valore di
TM.Il procedimente viene ripetuto fintantochè la
coppia di valori TM,TR soddisfa entrambe le
equazioni.Per quanto il software possa effettuare
calcoli di reti anche complesse ,per non appesantire
troppo il tempo di esecuzione si sostituisce lo schema
di figura 1 con quello equivalente ,aperto,
di figura 2.
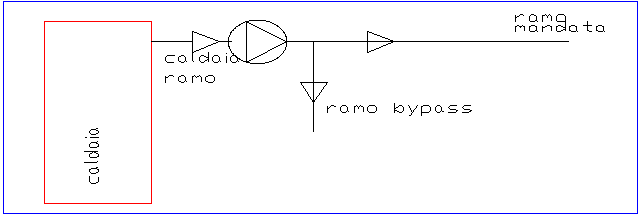
figura 2 : il circuito con valvola miscelatrice
modificato in circuito aperto
L’utenza e’ rappresentata da un unico corpo termico:
nel caso di radiatori l’emissione nominale e’ :9696
watt(esponente dell’emissione =1,3)
nel caso di ventilconvettori l’emissione nominale e’
13100 watt con una portata nominale di 1125 kg/h ed
una perdita nominale di 0,455 mt H2O
Il ramo mandata ha una lunghezza nulla ma in esso
viene inserita una valvola che simula la
caratteristica idraulica della rete a valle,la
caratteristica e’:
H= 0,295 x Q^1,899
Q ,portata,in mc/h
H ,prevalenza,in mt H2O
Il valore del KV max della valvola e’ :4
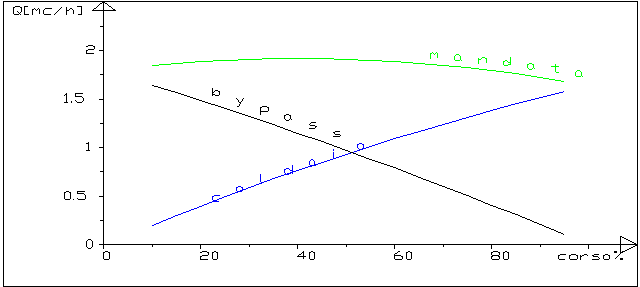
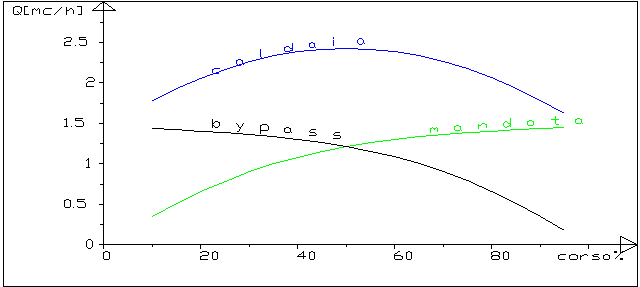
figura 3 : le portate nel circuito con valvola miscelatrice
(radiatori)
Il grafico di figura 3 rappresenta , al variare della
corsa della valvola miscelatrice(nel calcolo tra il
10% e il 95% ):
le portate nel ramo caldaia(caldaia),nel ramo di
bypass (bypass),nel ramo utenza (mandata),nel piano
corsa%-Q
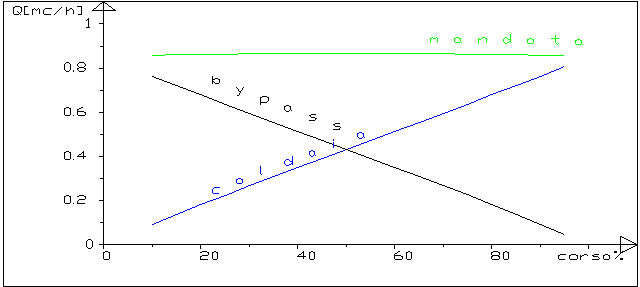
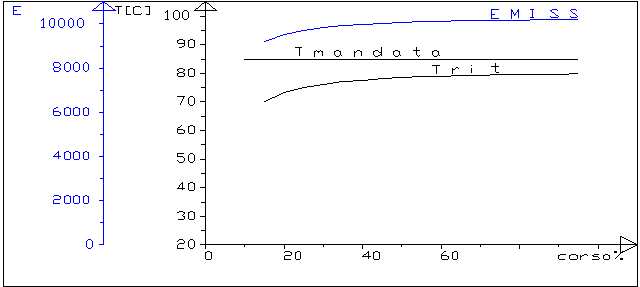
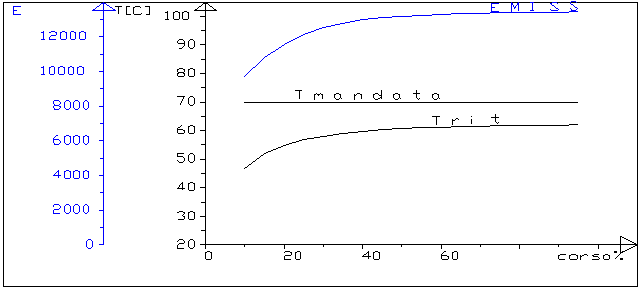
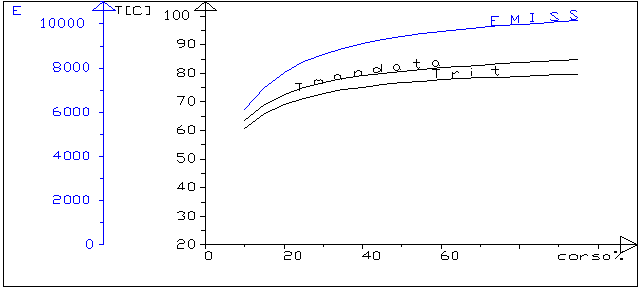
figura 4 : le emissioni nel circuito con valvola miscelatrice
(radiatori)
Il grafico di figura 4 rappresenta invece:
la temperatura di mandata (T mandata) e di ritorno( T
rit),nel piano corsa%-T
l’emissione(EMISS) ,nel piano corsa%-E
Si puo’ notare come:
nel ramo di mandata si realizzi una portata quasi
costante
le portate nel ramo bypass e nel ramo caldaia variano
approssimativamente nel rapporto secondo la [2]
la temperatura di mandata ,in conseguenza della
miscelazione aumenta all’apertura della valvola
l’emissione termica aumenta all’aumentare
dell’apertura
il salto termico aumenta leggermente all’aumentare
della corsa
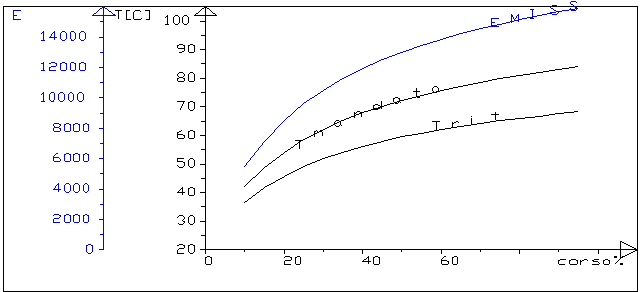
figura 5 : le emissioni nel circuito con valvola miscelatrice
(ventilconvettori)
figura 6 : le emissioni nel circuito con valvola miscelatrice
(ventilconvettori)
I grafici di figura 5 e 6 sono rappresentativi dello
stesso circuito ma con corpi termici
ventilconvettori.Si evidenzia subito la piu’ ripida
variazione sia della temperatura di mandata che
dell’emissione al variare della corsa.L’analisi dei
numerica dei risultati porta alle seguenti
considerazioni :
chiamiamo E10 l’emissione con corsa =10% e E95
l’emissione con corsa=95% sia inoltre:
DE=E95-E10
DE%=DE/E95
Q10 e Q95 :rispettivamente le portate con corsa 10% e corsa
95%
DQ=differenza fra la portata nel ramo di mandata con
corsa=95% e la portata con corsa=10%
DT=Tmandata con corsa=95% -Tmandata con
corsa=10%.
Raffrontando i risultati nei due casi,relativi alle
figure 6.7 e 6.8 si ha :
nel caso dei venticonvettori DE% e’ maggiore rispetto
ai radiatori: 66,8 anziche’ 42,4.Anche il rapporto
DE/DT e’ maggiore ,248 anziche’ 188.si puo’ arguire
che i ventilconvettori hanno una variazione di
emissione maggiore con la variazione della temperatura
di mandata rispetto ai radiatori.Di conseguenza il
circuito a ventilconvettori permette una regolazione
piu’ ampia dell’emissione . Si noti che la temperatura
di caldaia di 85’C e’stata fatta uguale anche per i
ventilconvettori per poter meglio effettuare il
confronto.
figura 7 : il circuito con valvola deviatrice
il circuito con valvola deviatrice
trasformato in aperto
REGOLAZIONE CON VALVOLA DEVIATRICE.
Lo schema
con valvola deviatrice e’ quello di figura 7.Anche in
questo caso,ai fini del calcolo,lo schema viene
sostituito con quello di figura 8,con le stesse
considerazioni fatte sopra.In tal caso la temperatura
di mandata (uguale a quella di caldaia) e’ costante
mentre varia la portata .Nel ramo caldaia la portata
non e’ costante .Le figure 9 e 10 (relative al
circuito con radiatori)riporta le stesse grandezze
delle figure precedenti ,mentre le figure 11 e 12
sono relative al caso dei ventilconvettori.E’
evidente che nel caso di radiatori l’azione regolante
viene a mancare.A variazioni consistenti della corsa
corrispondono piccole variazioni dell’emissione.Si ha
infatti numericamente nel caso dei radiatori DE%=17,6
contro 27,7 nel caso dei ventilconvettori.Il rapporto
DE/DQ ,fra la variazione di emissione e la variazione
di portata e’ invece 733 nel caso dei radiatori e
molto maggiore ,3546, nel caso di ventilconvettori.
Tutto questo conferma quanto già detto sull’emissione
termica dei radiatori e come questa sia influenzata
dalla portata in misura minore rispetto ai
ventilconvettori.
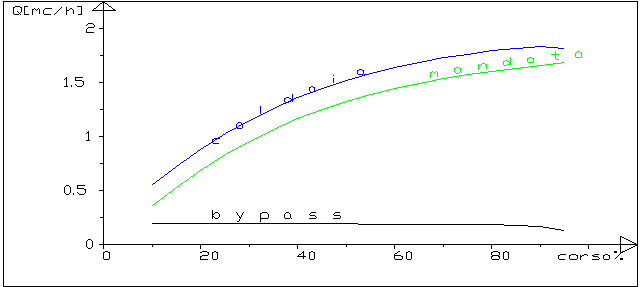
figura 9 : le portate nel circuito con valvola deviatrice
(radiatori)
figura 10 : le emissioni nel circuito con valvola deviatrice
(radiatori)
figura 11 : le portate nel circuito con valvola deviatrice
(ventilconvettori)
figura 12 : le emissioni nel circuito con valvola deviatrice
(radiatori)
L’INFLUENZA DEL VALORE KV.
Abbiamo gia’ detto come
una valvola regolatrice ha come grandezza
caratteristica KV.All’aumentare di KV la perdita di
carico della valvola diminuisce e viceversa.
Consideriamo il caso di valvola deviatrice
:se fosse KV molto grande le perdite di carico del
ramo caldaia sarebbero trascurabili e fra le prtate
del ramo caldaia Q3 e bypass Q2 si avrebbe la
relazione:
q3/q2=corsa/(1-corsa)
L’azione regolante della valvola sarebbe quindi
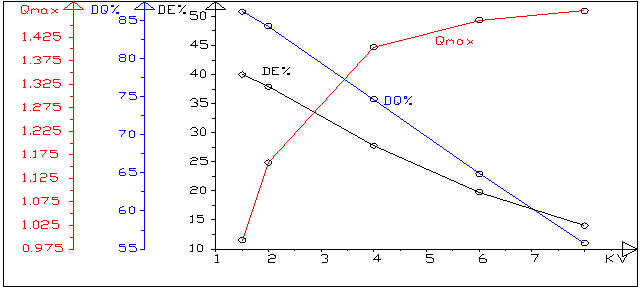
massima e propozionale alla corsa.Il grafico di figura
13 traduce sinteticamente i risultati del calcolo con
valvola deviatrice e ventilconvettori, per un valore
di KV variabile fra 2 ed 8,riportato in ascissa.In
ordinata viene riportato:
DE%= DE/E95
DQ%= Q10/DQ
Qmax= portata nel ramo mandata con corsa 95%
Si puo’ notare:
All’aumentare di Kvmax (e quindi minori perdite di
carico nella valvola)la variazione di emissione DE% e’
minore e quindi minore l’azione regolante.
Il rapporto Q10/DQ diventa maggiore ,si ha in pratica
una minor variazione di portata all’aumentare di
Kvmax(minori perdite di carico della
valvola) aumenta il valore di portata alla mandata
figura 13 : le variazioni di qmax, de% dQ% al variare di kv

AL MENU